飞机票：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=3204

题意：就是找两个点，使得路径上的点最多。

分析：刚看不知道从何下手，再仔细看看note就好了，note前半部分就是说图是连通的，因为说点是直接或则间接相连的，后半部分说明图没有环，因为说如果出去之后要回原来的点，必须经过一条至少两次。有这个的话就可以知道给的图是颗树，然后求树上两点之间的点数最多，即距离最大。那么可以用树形DP，假设当前的点为k，它的子树最大的深度为i和j，那么就可以知道当前的路径为i和j之间的和再加1（k这个点），然后更新MAX，然后把k和最大的子树路径递归上去，用来更新k的父节点就可以了，然后最后要判断MAX是否大于7，最后啪啪啪就可以AC了

/*
Author:Chieh
Because Of Coding
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <map>
#include <stack>
#define LL long long
#define INF 1e9
#define EPS 1e-9
using namespace std;
const int maxn=1234;
vector<int> V[maxn];
int n,m;
void init()
{
    for(int i=1; i<=n; i++)V[i].clear();
    int u,v;
    for(int i=1; i<n; i++)
    {
        scanf("%d%d",&u,&v);
        u++;
        v++;
        V[u].push_back(v);
        V[v].push_back(u);
    }
}
bool cmp(int a,int b)
{
    return a>b;
}
int MAX;
int DFS(int now,int fa)
{
    vector<int> need;
    need.push_back(0);
    need.push_back(0);
    for(int i=0; i<V[now].size(); i++)
    {
        int u=V[now][i];
        if(u==fa)continue;
        int p=DFS(u,now);
        need.push_back(p);
    }
    sort(need.begin(),need.end(),cmp);
    MAX=max(MAX,need[0]+need[1]+1);
    return need[0]+1;
}
void play()
{
    MAX=0;
    DFS(1,-1);
    if(MAX<7)printf("Impossible\n");
    else printf("%d\n",MAX);
}

int main()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        init();
        play();
    }
//    cout << "Hello world!" << endl;
    return 0;
}

飞机票：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=3127

题意：给你n个人n<=100，m辆车，n<=m<=100，然后给你n+m个坐标代表人和车的位置，最后再给你个速度v,求出最少的时间，使得每个人都有一辆车。(其中每个人都是同步进行的)

分析：这种题的话，就是相当于把n个人匹配到m辆车的n辆中，可以用二分图匹配算法，匈牙利的话是O（VE）那怎么求这个最少时间呢，其实可以二分求，然后每次二分的时间t，我们可以用O（nm）的时间，求的用t的时间，n个人可以和m辆车的哪几辆匹配，然后建图，跑一边匈牙利，如果可以最大匹配的话，那么这个时间是ok的，那么我们把上限变为t-0.001，因为要保留两位小数，反之把下限变为t+0.001，继续二分，最后输出答案即可。复杂的为logT*(n*m+VE),还是ok的，因为n和m比较小，最后啪啪啪就可以AC了

/*
Author:Chieh
Because Of Coding
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <map>
#include <stack>
#define LL long long
#define INF 1e9
#define EPS 1e-9
using namespace std;
const int maxn=123;
struct he
{
    double x,y;
} Sky[2][maxn];
int n,m;
double ai[maxn][maxn];
double l,r;
double calT(int i,int j,double v)
{
    double dis=sqrt((Sky[0][i].x-Sky[1][j].x)*(Sky[0][i].x-Sky[1][j].x)+(Sky[0][i].y-Sky[1][j].y)*(Sky[0][i].y-Sky[1][j].y));
    return dis/v;
}
void init()
{
    for(int i=1; i<=n; i++)scanf("%lf%lf",&Sky[0][i].x,&Sky[0][i].y);
    for(int i=1; i<=m; i++)scanf("%lf%lf",&Sky[1][i].x,&Sky[1][i].y);
    double v;
    scanf("%lf",&v);
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=m; j++)
        {
            ai[i][j]=calT(i,j,v);
        }
    }
    r=2000000.0/v;

}
bool bi[maxn][maxn];
int Link[maxn];
bool vis[maxn];
bool DFS(int now)
{
    for(int i=1; i<=m; i++)
    {
        if(bi[now][i]&&!vis[i])
        {
            vis[i]=1;
            if(Link[i]==0||DFS(Link[i]))
            {
                Link[i]=now;
                return true;
            }
        }
    }
    return false;
}
void play()
{
    double MIN=r;
    l=0;
    while(l<=r)
    {
        double mid=(l+r)/2;
        memset(bi,0,sizeof(bi));
        for(int i=1; i<=n; i++)
        {
            for(int j=1; j<=m; j++)
            {
                if(ai[i][j]<=mid)bi[i][j]=1;
            }
        }
        memset(Link,0,sizeof(Link));
        bool flag=1;
        for(int i=1; i<=n; i++)
        {
            memset(vis,0,sizeof(vis));
            if(DFS(i))continue;
            flag=0;
            break;
        }
        if(flag)
        {
            MIN=min(MIN,mid);
            r=mid-0.001;
        }
        else
        {
            l=mid+0.001;
        }

    }
    printf("%.2f\n",MIN);

}
int main()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        init();
        play();
    }
    //  cout << "Hello world!" << endl;
    return 0;
}

飞机票：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=3221

题意：就是给你6个正整数，前面三个是结果的数字，后面三个是起始的数字，我们可以从起始的数据选择一个数，然后删除它，用另外两个的和减去以代替，然后一直反复，看能否到达结果的三个数字。

分析：这种题一看，如果从初始状态推结果状态是很复杂的，因为每一次都有3个数字可以选择，所以复杂度肯定太高了，所以考虑用结果的三个数字推初始数据，因为假设结果数字为a1 a2 a2且a1<a2<a3，如果a1+a2-1=a3，说明a3是推过来的，所以可以把a3改回原来的数字，假设为a'3，那么a'3怎么算呢，因为我们知道现在a2最大，那么可以以为a1+a'3-1=a2,所以a'3=a2-a1+1,所以把a3换了，然后一直重复看看，能不能推到起始的三个数字。这里如果我们有a1+a2-1=a3的话，那么我们只要a1和a2能找到2个数字一样就可以了。因为a3可以变为任意数，然后的话如果a1+a2-1!=a3,那么特殊处理一下就行了，记得循环终止，如果a1+a2-1恒等于a3的时候，那么就可以终止了，因为死循环了，最后啪啪啪就可以AC了

/*
Author:Chieh
Because Of Coding
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <map>
#include <stack>
#define LL long long
#define INF 1e9
#define EPS 1e-9
using namespace std;
int ai[4],bi[4],T;
void init()
{
    for(int i=1; i<=3; i++)scanf("%d",&ai[i]);
    for(int i=1; i<=3; i++)scanf("%d",&bi[i]);

}
bool vis[4];
void play()
{
    while(1)
    {
        sort(ai+1,ai+4);
        sort(bi+1,bi+4);
        if(ai[1]+ai[2]-1!=ai[3])
        {
            if(ai[1]==bi[1]&&ai[2]==bi[2]&&ai[3]==bi[3])
            {
                printf("Yes\n");
                return;
            }
            else
            {
                printf("No\n");
                return;
            }
        }
        int sum=0;
        vis[1]=vis[2]=vis[3]=0;
        for(int i=1; i<=2; i++)
        {
            for(int j=1; j<=3; j++)
            {
                if(ai[i]==bi[j]&&!vis[j])
                {
                    vis[j]=1;
                    sum++;
                }
            }
        }
        if(sum>=2)
        {
            printf("Yes\n");
            return;
        }
        ai[3]=ai[2]+1-ai[1];
        if(ai[1]==1&&ai[2]==ai[3])break;

    }
    printf("No\n");
}
int main()
{
    scanf("%d",&T);
    while(T--)
    {
        init();
        play();
    }
    //cout << "Hello world!" << endl;
    return 0;
}

飞机票：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=3819

题意：就是有个人叫DD，他参见乒乓球比赛，然后要拿冠军，(就是赢得场数最多的人),给你m个初始的结果和下面还要比的场次，问DD能否拿冠军，其中只能有一个冠军(即不能有多个最大值)

分析:一看这道题，就知道贪心取DD能赢的最大值，即加入DD已经赢了p场，然后他下面还比了q场，贪心的话，他最多能赢p+q场，所以其余的人最多只能赢p+q-1场，因为不能有一样的最大值。先判断当前每个人已经赢了的场数，假设p+q=a1,别人当前赢得场数为a2。a3...an，如果a2到an其中有大于等于a1那么直接就是no了，因为不管怎么比，都不可能比a1小了如果都小于a1的话，就必须找个方法判断到底行不行？从前面可以知道第i个人最多只能赢a1-ai-1场，这样才小于a1,设为b2.b2..b3，然后假设第i个人和其他人除了DD一共比了k场，那么他最多只能赢bi场，因为限制。然后就是想什么方法判断每个人都满足。这里就用到了最大流算法。假设有个源点s，假如每对人i和j比了kij场，那么就有从s流kij的流量到i和j，我们可以定义为点vij,然后vij可以流向vi和vj，因为这个没有限制，但是可以定义为kij，因为最大了.最后我们可以定义个汇点，然后从vi流bi个流量到t，因为最大只能是bi，最后跑一边最大流，看它能不能是一个可行流，即除了和DD比的场数之外，所有的场数是否可以满足要求。最后啪啪啪就可以AC了。

/*
Author:Chieh
Because Of Coding
*/
/*
O(E^2 V)
E//边数
V//节点
//每次按最短的s-t路径进行增广
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <map>
#include <stack>
#include <queue>
#include <vector>
#define LL long long
#define INF 1e9
#define EPS 1e-9
using namespace std;
const int maxn=5*12;
map<string,int> M;
struct he
{
    int to,val,id;
};
vector<he> V[3000];
int n,m;
char ch1[12],ch2[12],ch3[12];
int win[maxn];
int next[maxn][maxn];
int Link[maxn][maxn];
void init()
{
    for(int i=1; i<3000; i++)
    {
        V[i].clear();
    }
    M.clear();
    ch1[1]='D';
    ch1[2]='D';
    ch1[3]='\0';
    M[ch1+1]=1;
    memset(win,0,sizeof(win));
    memset(next,0,sizeof(next));
    int st=1;
    for(int i=1; i<=m; i++)
    {
        scanf("%s%s%s",ch1+1,ch2+1,ch3+1);
        if(M[ch1+1]==0)
        {
            M[ch1+1]=++st;
        }
        if(M[ch2+1]==0)
        {
            M[ch2+1]=++st;
        }
        int t1=M[ch1+1];
        int t2=M[ch2+1];
        if(ch3[1]=='w')
        {
            win[t1]++;
        }
        else
        {
            win[t2]++;
        }
    }
    scanf("%d",&m);
    for(int i=1; i<=m; i++)
    {
        scanf("%s%s",ch1+1,ch2+1);
        if(M[ch1+1]==0)
        {
            M[ch1+1]=++st;
        }
        if(M[ch2+1]==0)
        {
            M[ch2+1]=++st;
        }
        int t1=M[ch1+1];
        int t2=M[ch2+1];
        if(t1>t2)swap(t1,t2);
        next[t1][t2]++;
    }
    for(int i=2; i<=n; i++)
    {
        win[1]+=next[1][i];
    }
}
int fa[3000];
int idx[3000];
bool vis[3000];
bool BFS(int s,int t)
{
    memset(vis,0,sizeof(vis));
    queue<int> Q;
    Q.push(s);
    fa[s]=s;
    vis[s]=1;
    while(!Q.empty())
    {
        int now=Q.front();
        Q.pop();
        if(now==t)return 1;
        for(int i=0; i<V[now].size(); i++)
        {
            int u=V[now][i].to;
            int w=V[now][i].val;
            if(w>0&&!vis[u])
            {
                vis[u]=1;
                fa[u]=now;
                idx[u]=i;
                Q.push(u);
            }
        }
    }
    return 0;
}
void play()
{
    for(int i=2; i<=n; i++)
    {
        if(win[i]>=win[1])
        {
            printf("No\n");
            return;
        }
    }//判断是否没开始就不能满足了
    int st=1;
    for(int i=2; i<=n; i++)
    {
        for(int j=i+1; j<=n; j++)
        {
            Link[i][j]=++st;
        }
    }
    for(int i=2; i<=n; i++)
    {
        Link[i][i]=++st;
    }
    st++;
    LL com=0;
    for(int i=2; i<=n; i++)
    {
        for(int j=i+1; j<=n; j++)
        {
            if(next[i][j]!=0)
            {
                int val=next[i][j];
                int v=Link[i][j];
                com+=val;
                V[1].push_back((he)
                {
                    v,val,V[v].size()
                });
                V[v].push_back((he)
                {
                    1,0,V[1].size()-1
                });
                int u1=Link[i][i];
                int u2=Link[j][j];
                V[v].push_back((he)
                {
                    u1,val,V[u1].size()
                });
                V[u1].push_back((he)
                {
                    v,0,V[v].size()-1
                });
                V[v].push_back((he)
                {
                    u2,val,V[u2].size()
                });
                V[u2].push_back((he)
                {
                    v,0,V[v].size()-1
                });
            }
        }
    }
    for(int i=2; i<=n; i++)
    {
        int id=Link[i][i];
        int val=win[1]-win[i]-1;
        V[id].push_back((he)
        {
            st,val,V[st].size()
        });
        V[st].push_back((he)
        {
            id,0,V[id].size()-1
        });
    }

    LL MAX=0;
    while(BFS(1,st))
    {
        int MIN=2*INF;
        int now=st;
        while(fa[now]!=now)
        {
            int f=fa[now];
            int id=idx[now];
            MIN=min(MIN,V[f][id].val);
            now=f;
        }
        MAX+=MIN;
        now=st;
        while(fa[now]!=now)
        {
            int f=fa[now];
            int id=idx[now];
            int idd=V[f][id].id;
            V[f][id].val-=MIN;
            V[now][idd].val+=MIN;
            now=f;
        }
    }
    if(MAX==com)printf("Yes\n");
    else printf("No\n");
}
int main()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        init();
        play();
    }
    // cout << "Hello world!" << endl;
    return 0;
}

飞机票：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=1891

题意：给你一个最终的数组，求初始数组，初始数组转化为最终数组的过程如下。假设有a1,a2...a8

第一次:a1+a2,a3+a4,a5+a6,a7+a8,a1-a2,a3-a4,a5-a6,a7-a8这八个数，

第二次:a1+a2+a3+a4,a5+a6+a7+a8,a1+a2-a3-a4,a5+a6-a7-a8,a1-a2,a3-a4,a5-a6,a7-a8,

第三次:a1+a2+a3+a4+a5+a6+a7+a8,a1+a2+a3+a4-a5-a6-a7-a7,a1+a2-a3-a4,a5+a6-a7,a8,a1-a2,a3-a4,a5-a6,a7,a8;

知道最后一项的第一项是从a1加到a8的时候停止，然后给你最终数列，即第三次的结构，求a1~a8,

分析：先从简单的开始，就拿例子直接来，可以发现我们加入可以把第三项推到第二项，然后把第二项推到第一项，最后把第一项还原成最初项，答案就出来了。怎么把第三项还原成第二项?可以发现第三项前面两项相加除2就是第二项的第一个，相减除2就是第二项的第二个，然后其余的不变。然后第二项怎么还原成第一项，发现第二项的第一个加第三个除以2是第一项的第一个，相减除以2是第一项的第二个，那么规律就有了。假设第三项为第一层，我们只把i从1枚举到层数，然后ai+ai+层数/2就是下面的相对应的项，ai-ai+层数/2也是相对应的项，怎么知道相对应的项，，我是来个下标计算的，因为每次都是增加两个，且是递增的，所以只要把下标进行改变就可以知道对应的是下一层哪个项了，其中我还有个辅助数组，因为如果ai在计算时就改变肯定会影响最终 结果计算完成后，层数就要乘以2，因为是2倍改变，然后就可以啪啪啪，AC了

/*
Author:Chieh
Because Of Coding
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#define LL long long
#define INF 1e9
#define EPS 1e-9
using namespace std;
const int maxn=300;
int n;
int ai[maxn];
int bi[maxn];
void init()
{
    for(int i=1; i<=n; i++)scanf("%d",&ai[i]);
}
int ci[]= {1,2,4,8,16,32,64,128,256};
void play()
{
    if(n==1)
    {
        printf("%d\n",ai[1]);
        return;
    }
    int e=0;
    for(int i=0; i<=8; i++)
    {
        if(ci[i]<<1==n)
        {
            e=i;
            break;
        }
    }
    for(int i=0; i<=e; i++)
    {
        int st=1;
        for(int j=1; j<=n; j++)bi[j]=ai[j];
        for(int j=1; j<=ci[i]; j++)
        {
            int p=(ai[j]+ai[j+ci[i]])>>1;
            int q=(ai[j]-ai[j+ci[i]])>>1;
            bi[st]=p;
            bi[st+1]=q;
            st=st+2;
        }
        for(int j=1; j<=n; j++)ai[j]=bi[j];
    }
    bool first=1;
    for(int i=1; i<=n; i++)
    {
        if(!first)printf(" ");
        first=0;
        printf("%d",ai[i]);
    }
    printf("\n");

}
int main()
{
    while(scanf("%d",&n)!=EOF)
    {
        if(n==0)break;
        init();
        play();
    }
//    cout << "Hello world!" << endl;
    return 0;
}

飞机票：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=1911

题意：就是给你一颗树包含n个点(n<=10000)和边权值，求任意两点之间的平均距离，即任意两点距离和除以有多少个点对。

分析：容易计算点对数就是n*(n-1)/2，如何求总距离和，可以考虑两个点，假设为u，v，且有条边(u,v)权值为x，这样我们就可以知道，x肯定要用u子节点的个数*v子节点的个数(其中子节点代表u下面所有的节点个数)，包含各自本身，因为u子节点到v子节点必定要经过(u,v）这条边，这样的话我们就可以递归处理了，假设当前节点为u，它的子节点数加它本身有p个，则它父亲节点v那一块就有n-p个。然后总距离就加上p*(n-p)*x了。最后啪啪啪，就可以AC了

/*
Author:Chieh
Because Of Coding
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <map>
#include <stack>
#include <queue>
#include <vector>
#define LL long long
#define INF 1e9
#define EPS 1e-9
using namespace std;
const int maxn=12345;
int T;
vector<int> V[maxn];
vector<int> G[maxn];
int n;
void init()
{
    int u, v,w;
    scanf("%d",&n);
    for(int i=1; i<=n; i++)
    {
        V[i].clear();
        G[i].clear();
    }
    for(int i=1; i<n; i++)
    {
        scanf("%d%d%d",&u,&v,&w);
        u++;
        v++;
        V[u].push_back(v);
        V[v].push_back(u);
        G[u].push_back(w);
        G[v].push_back(w);
    }
}
double ans;
int DFS(int now,int fa,double val)
{
    int chi=1;
    for(int i=0; i<V[now].size(); i++)
    {
        int u=V[now][i];
        int w=G[now][i];
        if(u==fa)continue;
        chi+=DFS(u,now,w);
    }
    int oth=n-chi;
    ans=ans+(val*oth*chi);
    return chi;
}
void play()
{
    ans=0;
    DFS(1,-1,0);
    double fm=(n*(n-1)/2);
    printf("%.10f\n",ans/fm);
}
int main()
{
    scanf("%d",&T);
    while(T--)
    {
        init();
        play();
    }
    //cout << "Hello world!" << endl;
    return 0;
}

飞机票： http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=4254

分析：其实这个题难懂的是题意啊~~~后来百度下骰子游戏菜知道这个题的意思。。先来看下骰子游戏的规则

规则略微有点复杂，刚开始可能不太明白，我详细解释下：

你的终极目标是占领所有的地块，你的颜色是紫色。
占领地块的方法就是用你的地块攻击相邻的地块，胜负由这两个地块上的骰子掷出点数决定。
1）如果你赢了，那么原来地块上的骰子变成一个，新占领地块上的骰子数 = 原来地块骰子数 - 1 ；
2）如果平了或者输了，那么你的地块上的骰子也会变成一个。
只要你的地块上的骰子数大于一个，就可以攻击别人。
在攻击结束时，点击 "End Turn" 可以补充兵力，补充的总数是你此时连在一起的地块的总数，分配则是随机的。每个地块上最多有 8 颗骰子。

提示策略：刚开始的时候尽量把自己的地都连到一起，中期的时候怎样布阵对于进攻和防守都很重要，后期基本都是八颗八颗的硬碰硬了 :P

看了应该就秒懂了吧。反正题目就是说给你攻击者的骰子数和防御者的骰子数。然后求攻击者赢得概率（就是说攻击者的点数严格大于防御者的点数）。。。这里要注意：如果攻击者的骰子数是1，那么就不能攻击，意思就是说赢得概率是0。。。然后你就可以根据概率来搞了。。。对于数学概率的渣渣，，，只有这么一个想法就是说把攻击者的点数枚举。。。怎么枚举法？？

已知n，那么攻击者的点数就是在n~6*n之间。。。然后枚举每个点数所占的概率。。。就是 k的可能方法有几种/6^n就是k的概率、、然后你要赢：那么就是m~6*m之间小于k的概率 那么就是(m~k-1)之间所有可能的方法/6^m的概率、、、然后从将所有的相加就是答案。。。这里计数方法，我先是DFS。。。其实也不慢，但是也不快。。。后来想到了DP。。。就是按骰子数来DP，然后当前骰子有6中可能1~6,然后看前面的是否出现过k,出现过，那么当前(k+(1~6））就要累加了。。。这样复杂度就直接变为(6*n)^2

/*
Author:Chieh
Grow up happy
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#include <map>
#define LL long long
using namespace std;
int ai[2][9][49];
int bi[2];
int p;
void play()
{
    if(bi[0]<=1)
    {
        printf("0\n");
        return;
    }
    for(int z=0; z<=1; z++)
    {
        int e=6*bi[z];
        memset(ai[z][0],0,sizeof(ai[z][0]));
        ai[z][0][0]=1;
        for(int j=1; j<=bi[z]; j++)
        {
            memset(ai[z][j],0,sizeof(ai[z][j]));
            for(int i=1; i<=6; i++)
            {
                for(int k=0; k<=e; k++)
                {
                    if(ai[z][j-1][k]>0)
                    {
                        ai[z][j][k+i]+=ai[z][j-1][k];
                    }
                }
            }
        }
    }
    int fm=pow(6.0,bi[0]);
    int fm1=pow(6.0,bi[1]);
    for(int i=1; i<=6*max(bi[0],bi[1]); i++)
    {
        ai[1][bi[1]][i]=ai[1][bi[1]][i]+ai[1][bi[1]][i-1];
    }
    double over=0;
    for(int i=1; i<=6*bi[0]; i++)
    {
        double pop=((double)(ai[0][bi[0]][i]))/fm;
        double pop1=((double)(ai[1][bi[1]][i-1]))/fm1;
        over=over+(pop*pop1);
    }
    printf("%.8lf\n",over);
}
int main()
{
    while(scanf("%d%d",&bi[0],&bi[1])!=EOF)
    {
        play();
    }
    return 0;
}

飞机票： http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=990

由于昨天有事。。。所以没怎么细想。。。然后一直以为只要深度相同。。。然后子节点个数相同就可以了。。。然后就一直Wa。。。后来自己把自己的想法推翻了。。。直接看下图：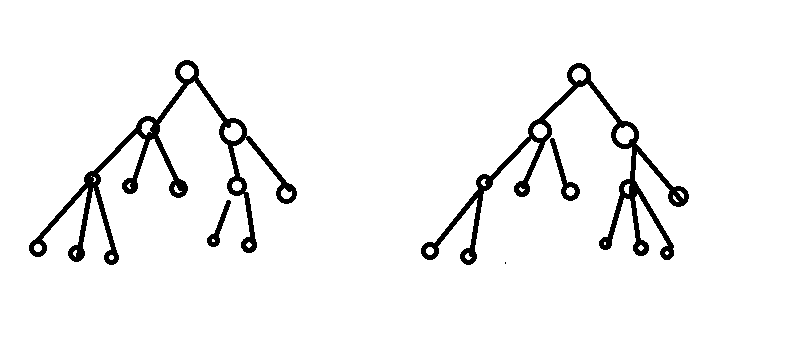

然后这里的话。。。如果按我起先的想法肯定是wa的因为1层都有2个子节点。二层有3个节点和2个节点。三层有2，0，0，3，0个节点

但是这两棵树明显不同、、debug爽啊。。。接着我的想法就是。。。那把每个节点的深度算出来和他的子树节点的深度都算出来。。。然后排序比较。。。这个想法明显是正确。。但是速度不快啊~~~囧。然后百度了一下。。。有一种方法是跟括号匹配差不多。。。就是说经过父节点（，回到了父节点就），然后括号里面的可以交换位置。。。交换出最小字典序。。。然后比较是否相同，还有一种方法：好像说是只要把深度算出来然后计算子树节点数排序比较就可以了。。。但是为什么呢。。感觉也不怎么对。。。画个图。。。其实这个想法是错误的

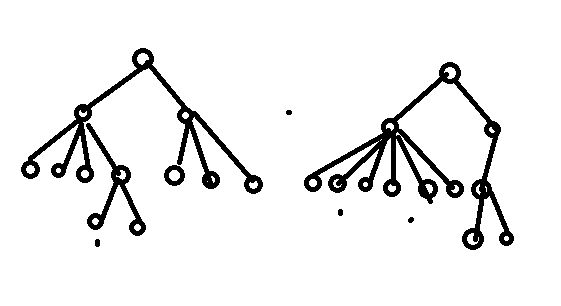
这个的序列是0010101001011100101011和0010101010101100010111。。。然而这个是diff。但是前面的跑出来的是same。。所以错误的。。。估计测试数据没有这个数据。我还是不传输错误的代码了。。。就用那个速度慢的吧

/*
Author:Chieh
Grow up happy
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
#include <map>
#include <vector>
#include <stack>
#define LL long long
using namespace std;
const int maxn=3456;
char ch[2][maxn];
struct he
{
    int dep;
    vector<int> V;
} JLJ[2][1567];
void init()
{
    scanf("%s%s",ch[0]+1,ch[1]+1);
}
int idx,st, p;
int len;
void DFS(int now,int dep)
{
    JLJ[p][now].dep=dep;
    while(idx<=len&&ch[p][idx]=='0')
    {
        idx++;
        st++;
        int q=st;
        DFS(q,dep+1);
        for(int j=0; j<JLJ[p][q].V.size(); j++)
        {
            JLJ[p][now].V.push_back(JLJ[p][q].V[j]+1);
        }
    }

    JLJ[p][now].V.push_back(0);
    sort(JLJ[p][now].V.begin(),JLJ[p][now].V.end());
    idx++;
    return;

}
bool cmp(he a,he b)
{
    if(a.dep!=b.dep)return a.dep<b.dep;
    if(a.V.size()!=b.V.size())return a.V.size()<b.V.size();
    for(int i=0; i<a.V.size(); i++)
    {
        if(a.V[i]>b.V[i])
        {
            return 1;
        }
        else if(a.V[i]<b.V[i])
        {
            return 0;
        }
    }
    return 0;
}
void play()
{
    if(strlen(ch[0]+1)!=strlen(ch[1]+1))
    {
        printf("different\n");
        return;
    }
    len=strlen(ch[0]+1);
    for(int i=0; i<=len/2; i++)
    {
        JLJ[0][i].dep=0;
        JLJ[0][i].V.clear();
        JLJ[1][i].dep=0;
        JLJ[1][i].V.clear();
    }
    idx=1;
    st=0;
    p=0;
    DFS(0,0);
    idx=1;
    st=0;
    p=1;
    DFS(0,0);
    sort(JLJ[0],JLJ[0]+st+1,cmp);
    sort(JLJ[1],JLJ[1]+st+1,cmp);
    //cout<<st<<endl;
    for(int i=0; i<=st; i++)
    {
        if(JLJ[0][i].dep!=JLJ[1][i].dep)
        {
            printf("different\n");
            return;
        }
        if(JLJ[0][i].V.size()!=JLJ[1][i].V.size())
        {
            printf("different\n");
            return;
        }
        for(int j=0; j<JLJ[0][i].V.size(); j++)
        {
            if(JLJ[0][i].V[j]!=JLJ[1][i].V[j])
            {
                printf("different\n");
                return;
            }
        }

    }
    printf("same\n");
}
int n;
int main()
{
    scanf("%d",&n);
    for(int i=1; i<=n; i++)
    {
        init();
        play();
    }
    //cout << "Hello world!" << endl;
    return 0;
}

飞机票： http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=4888

分析：起先想要把所有可能求出来。。。然后二分答案。。。但是内存不够呀然后各种优化啊。。。还是不行啊。。。果然是彩笔~接着就想着暴力。。。暴力你妹啊！！！各种TLE啊~~~没办法了。。想着在线二分。。。但是二分k还是r呢。。。第一直觉是k。。然后就往k里面想了。。。发现k无法正常二分。。。必需要有什么东西可以限制k的大小就可以二分。。。想想r不是很小么40...那就用r来限制k二分。。。接着就是各种悲剧渣死了。。。各种Wa。。。后来看了别人的题解。。。发现我二分里面有些是多余的。。。果然是自己贱啊但是想法还是正确的。。最后改了几个地方就AC了

/*
Author:Chieh
Grow up happy
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
#include <map>
#include <stack>
#include <vector>
#define LL long long
using namespace std;
LL n;
LL cal(int e)
{
    LL l=2,r=min(n,1000000LL);
    while(l<=r)
    {
        LL mid=(l+r)/2;
        LL over=1;
        LL tm=1;
        for(int i=1; i<=e; i++)
        {
            tm=tm*mid;
            over+=tm;
            if(over>n+1)break;
        }
        if(over==n+1||over==n)return mid;
        if(over>n+1)r=mid-1;
        else
        {
            l=mid+1;
        }
    }
    return 0;
}
void play()
{
    LL a=1,b=n-1;
    for(int i=2; i<=39; i++)
    {
        LL t=cal(i);
        if(t==0)continue;
        if(t*i<a*b)
        {
            a=i;
            b=t;
        }
        else if(t*i==a*b)
        {
            if(a>i)
            {
                a=i;
                b=t;
            }
        }
    }
    printf("%lld %lld\n",a,b);
}
int main()
{

    while(scanf("%lld",&n)!=EOF)
    {
        play();
    }
    return 0;
}

飞机票： http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=4106

今天起来一道2-sat。。。巩固知识~~~

分析：题目的意思就是说求函数最大能递归到第几层。。。告诉你a,b,c数组。。。x数组未知。。。题目秒懂。。。那个程序就不解释了，ACMer肯定能够看得懂:).这种题该怎么搞？？其实这里发现一个限制递归的地方就是

if dep < m and x[a[dep]] + x[b[dep]]
 != c[dep] then go(dep + 1, n, m)

那个<m就不用讲了。。如果>=m就溢出a,b,c数组了。。。那么其实就是后面的那个条件。。。我们二分0~（m-1）。假设当前的值是mid。。。那么就可以加边了。。。循环从0~mid。。。取出a[k]和b[k],c[k]的值（语文有限。。。望看懂~）那么如果c[k]的值是0.那么x[a[k]]+x[b[k]]的值至少有一个是1 如果是c[k]是1 那么两个值必须相同。。。如果是2 那么两个值肯定不同。。这里发现其实这个跟那个位运算2-sat题型差不多。。。然后把边添加了跑一下tarjan。。。如果不行。。说明递归层太深、、、r=mid-1.如果可以，那么l=mid+1...这样找到最大值即可~啪啪啪。。。TLE（vector忘记清0了。。。bug啊！！！）最后只要把深度+1就可以AC了

/*
Author:Chieh
Grow up happy
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <map>
#include <queue>
#include <stack>
#include <vector>
#define LL long long
using namespace std;
const int maxn=456;
const int Maxn=12345;
struct he
{
    int a,b,c;
} JLJ[Maxn];
vector<int> V[maxn];
int n,m;
void init()
{
    scanf("%d%d",&n,&m);
    for(int i=0; i<m; i++)
    {
        scanf("%d%d%d",&JLJ[i].a,&JLJ[i].b,&JLJ[i].c);
    }
}
bool instack[maxn];
int dfn[maxn],low[maxn],sta[maxn],belong[maxn],indexx,scnt,cntnum;
void tarjan(int u)
{
    dfn[u]=low[u]=indexx++;
    instack[u]=1;
    sta[++scnt]=u;
    for(int i=0; i<V[u].size(); i++)
    {

        int v=V[u][i];
        if(dfn[v]==-1)
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(instack[v])low[u]=min(dfn[v],low[u]);
    }
    if(dfn[u]==low[u])
    {
        for(int v=-1; v!=u; scnt--)
        {
            v=sta[scnt];
            instack[v]=0;
            belong[v]=cntnum;
        }
        cntnum++;
    }
}
void play()
{
    int l=0;
    int r=m-1;
    int over=0;
    while(l<=r)
    {
        int mid=(l+r)/2;
        for(int i=0;i<=2*n;i++)V[i].clear();
        for(int i=0; i<=mid; i++)
        {
            int u=JLJ[i].a*2;
            int v=JLJ[i].b*2;
            int t=JLJ[i].c;
            if(t==2)
            {
                V[u].push_back(v^1);
                V[v].push_back(u^1);
            }
            else if(t==1)
            {
                V[u].push_back(v);
                V[v].push_back(u);
                V[u^1].push_back(v^1);
                V[v^1].push_back(u^1);
            }
            else
            {
                V[u^1].push_back(v);
                V[v^1].push_back(u);
            }
        }
        indexx=cntnum=0;
        scnt=-1;
        memset(dfn,-1,sizeof(dfn));
        memset(instack,0,sizeof(instack));
        for(int i=0; i<2*n; i++)
        {
            if(dfn[i]==-1)tarjan(i);
        }
        bool flag=1;
        for(int i=0; i<n; i++)
        {
            if(belong[i*2]==belong[i*2+1])
            {
                flag=0;
                break;
            }
        }
        if(!flag)
        {
            r=mid-1;
            continue;
        }
        over=max(over,mid);
        l=mid+1;
    }
    printf("%d\n",over+1);

}
int T;
int main()
{
    scanf("%d",&T);
    while(T--)
    {
        init();
        play();
    }
    //  cout << "Hello world!" << endl;
    return 0;
}